深度学习笔记（二）神经网络法实现简单的线性回归

本文是用神经网络的方式来解决一元线性回归问题，主要是展现下训练的过程。

1 拟合的步骤

• 初始化”常量”，也即权重值，训练就是不断修改它，达到最优解
• 将变量输入公式得到结果
• 根据输出结果和实际结果得到误差
• 将误差反向传递更新权重值
• 是否误差达到了容忍值，没有则继续输入新变量，继续调整

2 概念

2.1权重

作为神经元的参数，输入数据进过它得到结果，所有当结果有误差时候，会对它进行调节

2.2梯度下降

梯度下降是在损失函数基础上向着损失最小的点靠近而指引了网络权重调整的方向

2.3损失函数

损失表示是的是所以样本的误差，例如很多个点拟合成线时，要求所以点的误差最小才行
损失函数的作用是计算神经网络每次迭代的前向计算结果与真实值的差距，从而指导下一步的训练向正确的方向进行。

3 方程

3.1 网络

一个神经元的单层网络，定义预测公式，也即是最终拟合直线的公式：
y = ax + b
公式里x，y是变量，a和b是常量，但这里把ab叫做权重，y是模型预测输出，x是输入

3.2 损失函数

这里用均方差作为损失函数
loss(a,b) = 1/2 (z - y)**2
其中z是计划的输出，y是实际的输出

3.3 反向传递

反向传递即是通过误差来修正权重
现在需要得到权重与误差的关系， 也即计算梯度
w的梯度 = 损失函数loos中w的偏导数：
(z - y) * x
b的偏导：
z-y

3.4 与最小二乘法

到这里其实就感觉深度学习和最小二乘法非常相似，他们都属于机器学习，也是解决回归问题的有效方法。

最小二乘法是常见回归算法，基于最小化误差平方和预测目标值。它的基本思想是通过对训练数据的拟合来得到一个预测函数，这个预测函数能够最好地描述训练数据。最小二乘法假设预测函数为一个线性函数，并通过最小化误差平方和来找到模型参数。
深度学习则是一种基于多层神经网络的机器学习方法，其中每一层可以看作是一个特征提取器。深度学习不同于最小二乘法，它能够处理非线性的问题，也不需要假设预测函数的形式。深度学习对于大规模数据集有着极强的学习能力，可以自动从原始数据中提取特征，从而得到高精度的预测结果。
总的来说，最小二乘法和深度学习都是有效的回归算法，但深度学习在处理非线性和大规模数据方面有着更强的能力。

4 代码

net.py

class NeuralNet:
    def __init__(self,eta):
        self.eta  = eta #学习率，也即是w和b的变化程度
        self.w = 0
        self.b = 0
        self.best = {"loss":0, "w":0, "b":0}
    
    # 向前传播
    def __forward(self,x):
        return self.w * x + self.b  # z = wx + b

    # 反向传播，得到wb的梯度
    # 损失  loss(w,b) = 1/2 * (z - y)**2  z表示实际结果，y表示预测结果，做均方差
    # dw = (z -y)x
    # db = (z-y)
    def __backward(self,x,y,z):
        dz = z - y # 中间变量 防止重复
        dw = dz * x
        db = dz
        return dw,db

    #梯度更新
    def __update(self,dw,db):
        self.w -= self.eta * dw
        self.b -= self.eta * db
        print("w:{},b:{}".format(round(self.w,2),round(self.b,2)))
    
    # x是输入，y是实际结果，z是推理结果
    def train(self, xList,yList):
        zList = []
        for i in range(len(xList)):
            # get z from x,y
            z = self.__forward(xList[i])
            # 保留2位小数
            z = round(z,2)
            zList.append(z)
            # calculate gradient of w and b
            dw, db = self.__backward(xList[i], xList[i], z)
            # update w,b
            self.__update(dw, db)
            loss = 0.5 * (z - yList[i])**2
            print("第{}轮计算，输入：{}，输出：{}，实际：{} loss：{},dw：{}，db：{}".format(i,xList[i],z,yList[i],round(loss,2),round(dw,2),round(db,2)))
            if(self.best["loss"] == 0):
                self.best["loss"] = 0.5 * (z - yList[i])**2
            else:
                if(self.best["loss"] > 0.5 * (z - yList[i])**2):
                    self.best["loss"] = 0.5 * (z - yList[i])**2
                    self.best["w"] = self.w
                    self.best["b"] = self.b

        return self.best["w"],self.best["b"],zList
    
    #预测
    def inference(self, x):
        return self.__forward(x)

app.py

from NeuralNet import NeuralNet

def readData(data_dir):
    xList = []
    yList = []
    with open(data_dir) as f:
        dir_labels = [line.strip().split('\t') for line in f.readlines()]
    for x, y in dir_labels:
        xList.append(x)
        yList.append(y)
    return xList, yList

import matplotlib.pyplot as plt

if __name__ == '__main__':
    xList,yList = readData("./tempData.txt")
    # 转浮点数
    xList = [float(x) for x in xList]
    yList = [float(y) for y in yList]
    net = NeuralNet(0.005)
    bestW,bestB,zList = net.train(xList,yList)
    print(net.w,net.b)
    plt.scatter(xList,yList)
    plt.scatter(xList,zList,color="red")
    newX = [1,13]
    newY = [net.w * x + net.b for x in newX] 
    plt.plot(newX ,newY)
    bestX = [1,13]
    bestY = [bestW * x + bestB for x in bestX]
    plt.plot(bestX,bestY,color="red")
    plt.show()

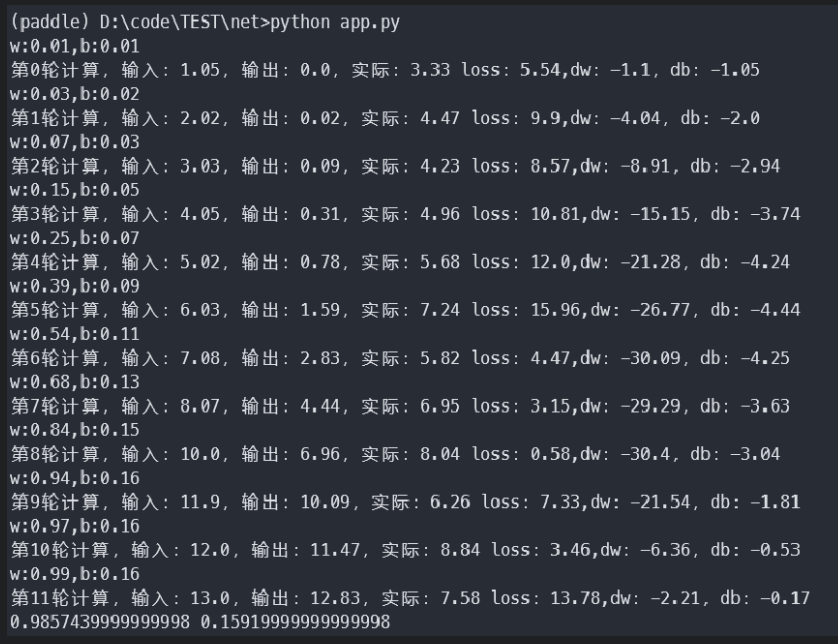
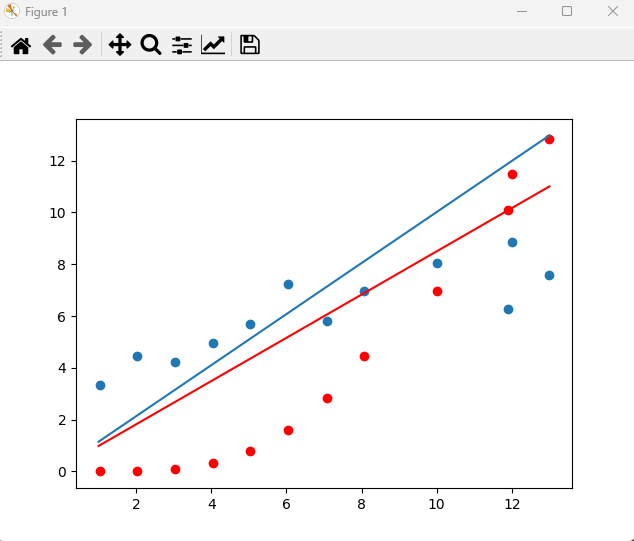
5 结果